Methods for Measuring Resolution and 50% MTF

Resolution
Resolution tests were run with the Canon EOS 400D Digital Rebel XTi and with a Canon EOS-1Ds Mark II at a working distance that filled the viewfinder of the EOS-1Ds with the target An Edmund Scientific lens resolution chart with several overlain Koren 2003 lens test charts at different angles was illuminated with two tungsten modeling bulbs from monolight flashes. The lenses and camera were mounted on a Bogen 3033/Arca Swiss B1 tripod/head combination with a large Kirk bean bag weighing down the tripod/head to dampen vibration. Three exposures using aperture priority exposure and +1.3 exposure compensation were taken at each aperture via cable shutter release at ISO 100 in RAW mode. The central autofocus point was centered over the center pattern for each exposure. The lens was defocused, and then refocused using autofocus for each exposure. RAW files were converted to 300 dpi 8-bit tifs with Capture One Pro v 3.76 software, and images were analyzed in Photoshop. Measurements were made from the sharpest image of the three taken.

Measurement were made at the center pattern, a middle pattern, and the edge pattern as shown here. Both line patterns at 90° angles had to be clearly visible. The highest resolution score for each aperture in the best of two photos taken at each aperture was recorded to minimize the the effect of potential autofocus error. Center-weighted resolution was calculated (60% center; 30% middle; 10% edge). Resolutions (lpm) at each f/stop were calculated using the method on the chart as follows.

Image lines pairs per mm (image lpm or lp/mm) = lpm resolved on chart X (D-fo) / fo) where fo = focal length of lens and D = Distance from the chart to the middle of the lens.

50% MTF (modulation transfer function):
There is general agreement that perceived image sharpness is more closely related to the spatial frequency (lp/mm) where MTF is 50% (i.e., where contrast has dropped by half) than to resolution alone. I used the Koren 2003 lens test chart developed and explained by Norman Koren to calculate 50% MTF. Printed test charts were placed on the Edmund Scientific Test Chart as in the middle and edge of the chart as shown here. The same photographs are used to measure resolution and 50% MTF. Measures of 50% MTF were calculated using the center pattern only. Because 50% MTF was measured only using the center chart the 50% MTF values can only be compared among lenses tested in this review section.


The imaged sine patterns were analyzed with and measurements were made on the resulting Plot Profile to determine line pair per mm frequency of 50% contrast as explained in detail on the Norman Koren website.

Details of calculating 50% MTF:

1. The 5mm Koren 2003 lens test chart designed to be printed at 25 cm long (50X magnification) was downloaded from the Koren website and printed on semi-gloss paper with a Epson 1270 printer at 1440 dpi. Charts are trimmed and mounted on the Edmund Scientific Test Chart as shown:



2. The chart is photographed at a working distance that is close to 1/2 the recommended distance so that the entire Edmund Scientific chart can be photographed for resolution and determination of 50% MTF.

3. The tif files are opened in image analysis software to analyze the sine patterns on the chart (top band). I used ImageJ software, public domain software off the NIH site.



Click on "File" and then "Open" to select and open the tif of interest. A scale image will be displayed.

4. Click on the "magnifying cursor symbol" to fill the window with the Koren chart image and click on the "hand" icon to move the chart image into the middle of the window.

5. Click on the line icon and draw a straight line through the upper sine pattern bar on the Koren chart.



6. Click on the "Analyze" menu and select "set scale" and enter "known distance" as "25" and "units" as "cm".

7. Click on "Analyze" again and select "Plot Profile."

8. A sine wave pattern will be generated and displayed.



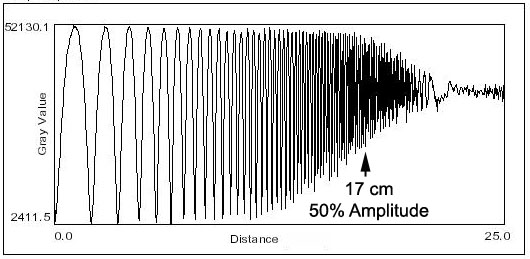
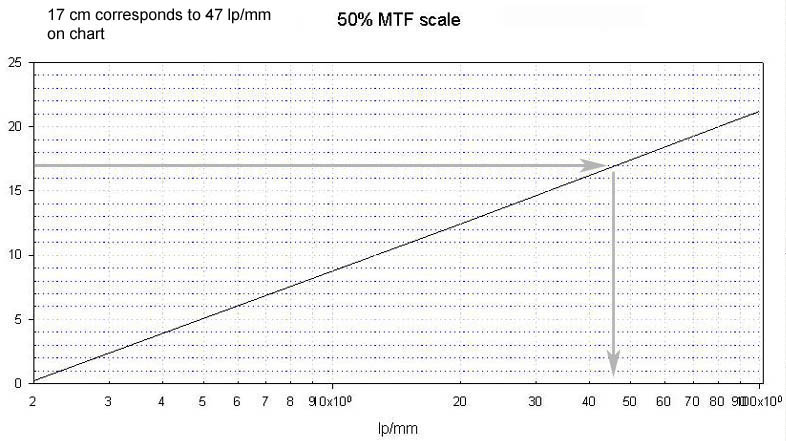
9. The full amplitude of the sine wave on my computer screen has a 7 cm sweep. I just take a rule and run it down the plot towards 25cm until the amplitude is 50% (3.5 cm). In the example, 50% amplitude is at 17 cm on the chart. This corresponds on a plot of cm of chart versus a log plot of spatial frequency below to 47 lp/mm.